在衡量风险的指标上,标准差(Standard Deviation,简称std,符号σ)比方差使用更广泛,其计算公式如下:
标准差即为方差的开根号。聪明的朋友们一下子想明白了,图形上其代表的就是正方形的边长,表征的是收益率的离散程度。标准差还有一个名字叫波动率,做期权的朋友一定很熟悉了。标准差一般用百分比表示,以年化计。
标准差如何年化:我们知道收益率有日收益率、周收益率、月收益率和年收益率,我们之前的aapl表格使用的是月收益率。这些收益率年化的计算公式如下:
σ年化=σ日*sqrt(252)
σ年化=σ周*sqrt(52)
σ年化=σ月*sqrt(12)
sqrt()是开根号函数。
我们回到AAPL.csv,在K2单元格输入=SQRT(J2)*SQRT(12),J2是我们之前计算出的方差值。因为我们在雅虎财经取的是AAPL月收益率,所以计算年化需要乘以SQRT(12),得出的值为29.9%。
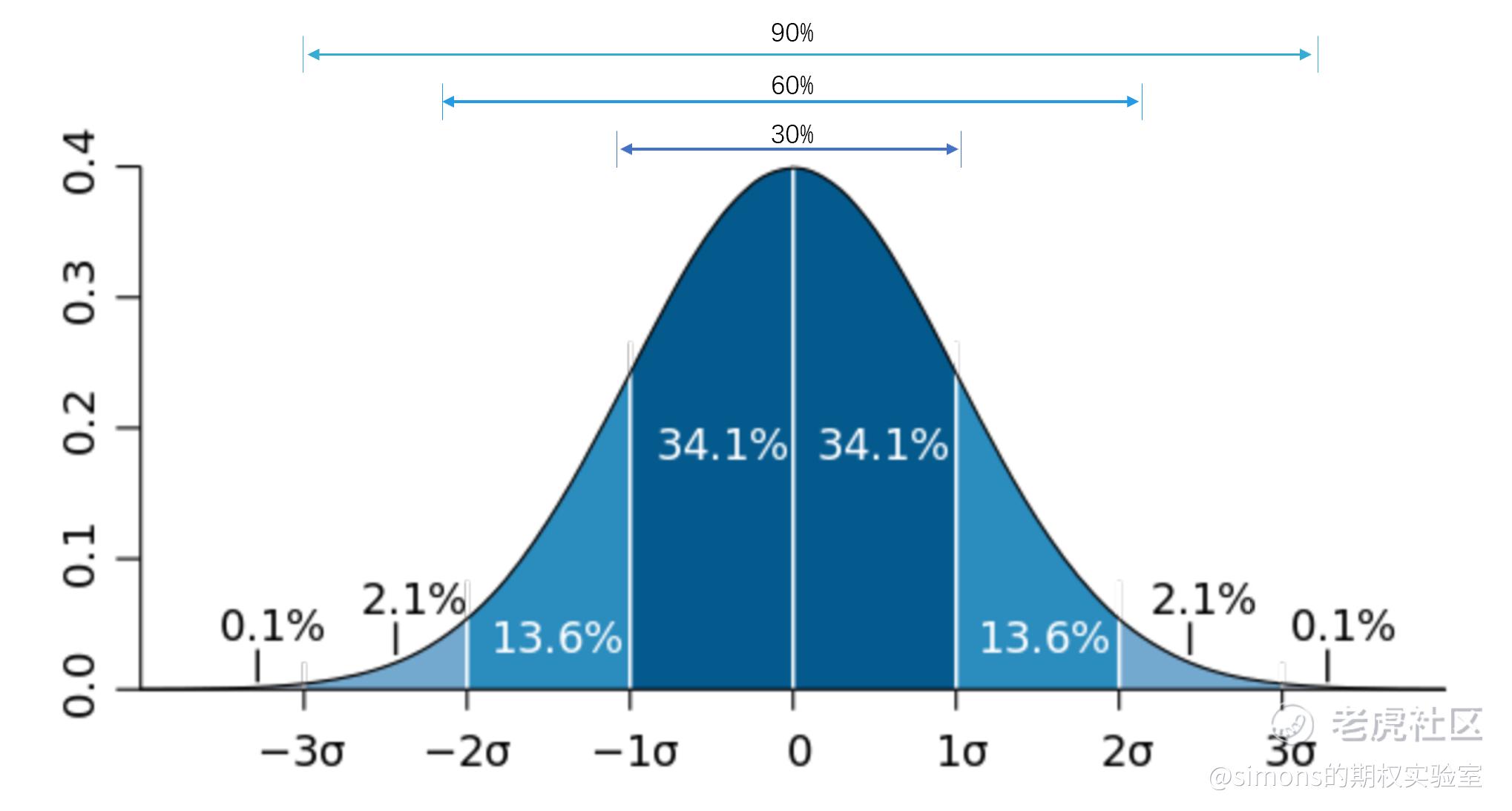
得出的29.9%的标准差是什么概念呢(下面近似成30%)?这是我们进入概率论和统计学的范畴。我们将各时间的收益率作图,其分布图形如下,为典型的正态分布。(例子中我们只引用了43个月的数据,数据量偏少,有兴趣的朋友可以多下载数据用excel直方图画正态分布,这里跳过。)
根据此图及概率论的数学期望告诉我们:AAPL在未来一年内上涨或下跌30%以内的概率为68.3%,上涨或下跌60%以内的概率为95.5%,上涨或下跌90%以内的概率为99.3%。不要觉得这些数字不可能,AAPL3月份的时候就回撤过30%以上。
从这里,我们可以知道σ越大,相同的概率下期望下跌的范围越大。所以说标准差是衡量风险的最重要指标。σ越大,输钱的概率越大。
以下是几个主要资产或股票的10年标准差数据(从高到低),可以参考,不同资产有不用的风险属性。
顺便一句,标准差即为股票的历史波动率,通过期权价格和收益率根据BS公式推算的为隐含波动率,有异曲同工之妙,这个我们后期再谈。$债券20+美公债指数ETF-iShares(TLT)$ $SPDR黄金ETF(GLD)$ $美元ETF-PowerShares DB(UUP)$


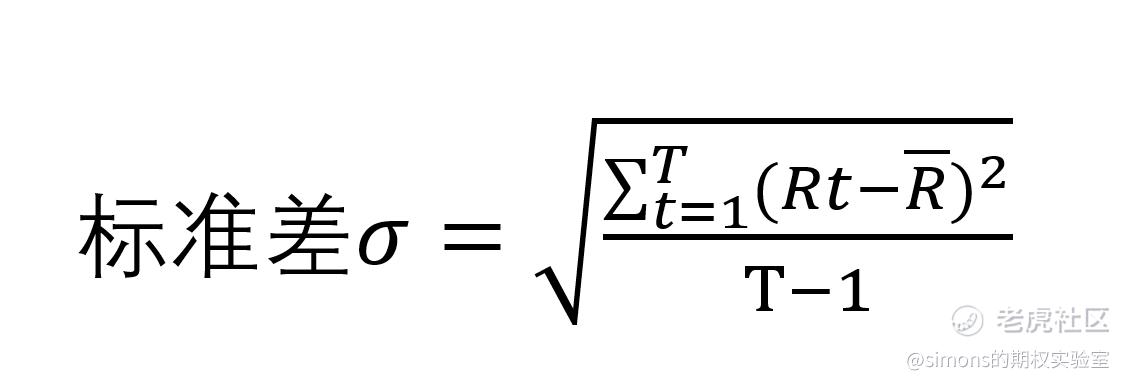

精彩评论