社区

如果说要从投资界找出一条最速曲线的话，那也就“凯利公式”莫属了。很多人都喜欢研究凯利公式，一是它的实用性，二是它的名气。

文章转载自公众号“三位一体股市赢家”

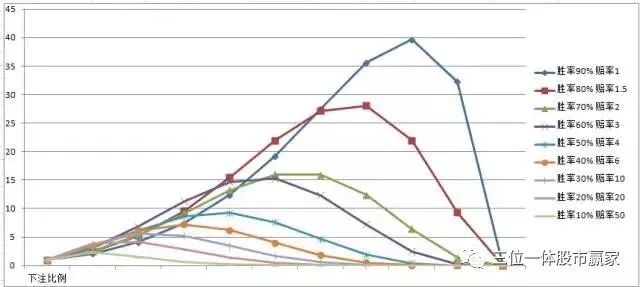
基本都懂，凯利公式是研究胜率赔率以及仓位（也就是下注金额）的关系。凯利公式：f=(bp-q)b (p是胜率 q是败率 b是赔率)，

如果单说高胜率，高赔率。那肯定两者双高是最好的结果。可是，往往这高并不太可能同时存在。熊掌和鱼不可兼得。

一般来说，喜欢孤注一掷的，无形中高赔率；喜欢积小成多的，选择无形中选择高胜率。

举个例子。

胜率90% 赔率1胜率50% 赔率4胜率10% 赔率50 胜率90% 赔率1 f=(1*0.9-0.1)/1=0.8 胜率50% 赔率4 f=(4*0.5-0.5)/4=0.375 胜率10% 赔率50 f=(50*0.1-0.9)/50=0.082

这是假设胜率赔率情况下的最佳下注比例。

很明显，如果都严格采用凯利公式仓位下注的话，假设胜负结果都一样的话，次数越多，胜率高的结果就越比胜率低的结果优秀。

放在股市里，换句话说，理论上，做短线的人，往往摆脱不了均值回归。

不过，在股市里，值得注意的地方，概率并不是孤立存在。也就是说，一副牌抽出去又放回来，再抽的概率是一样的。而股市里，并不是独立存在的。比如今天的上涨下跌就很可能和昨天的上涨或者下跌有关，也有可能跟消息面有关。就造成了一系列的变动。也就是所谓的“肥尾效应”。

什么是肥尾效应。是指极端行情发生的机率增加，可能因为发生一些不寻常的事件造成市场上大震荡。翻译过来也就是，从长期看，小概率的事件肯定会是必然发生的。

所以往往我们在实际操作行为当中，总以为小概率事件跟我们没有关系。但老股民都知道，时间越长，小概率碰到的就越多。诸如突然停牌，诸如个股类的黑天鹅等等。一旦遇到这种，如果仓位不对，将会产生很大的回撤。

因此，凯利公式还给我们一个启发就是，它不仅仅是在提高收益率，更多的是在控制风险。

$伯克希尔(BRK.A)$ $伯克希尔B(BRK.B)$