现代资产组合论

此篇不是CFA教材，请放心阅读。内有干货，中途不宜走开。

自投资的远古时期，人们认为：选股票就如同选美一样，挑选几个自己认为“最美”的股票进行投资。这就是“凯恩斯选美论”。

1952年，美国经济学家马可维茨（Harry M．Markowit）在他的学术论文《资产选择：有效的多样化》中，首次应用资产组合报酬的均值和方差这两个数学概念，从数学上明确地定义了投资者偏好，并以数学化的方式解释投资分散化原理，系统地阐述了资产组合和选择问题，标志着现代资产组合理论（Modern Portfolio Theory，简称MPT）的开端。该理论认为，投资组合能降低非系统性风险，一个投资组合是由组成的各证券及其权重所确定，选择不相关的证券应是构建投资组合的目标。

虽然现代资产组合理论做了很多在现实市场中并不存在的理想化假设，使得该理论无法在投资实践中得到普遍应用，但它在传统投资回报的基础上第一次提出了风险的概念，认为风险而不是回报，是整个投资过程的重心，并提出了投资组合的优化方法，马可维茨因此而获得了1990年诺贝尔经济学奖。

马可维茨提出的分散化（diversified）是该理论核心内容。一个分散化的投资组合的波动率远比各个单项投资的波动率之和低。

其实其原理很简单，我们在初中物理就学过波的叠加，相位相同的波叠加后波动更剧烈，相位相反的波会相互抵消。我们把波看成收益曲线后，集中投资同一领域的几只股票波动会叠加，分散化后波动率会抵消。

“不能把鸡蛋放在一个篮子里”，这是交易世界里一句流行的俗语。但是重仓或满仓1只股票的“惨案”还是时常发生。其投资的逻辑遵循的是“选美论”，也许也会选到AAPL、AMZN这样的“美女”，但不曾想却是个渣男，在”美女”表现不佳的时候弃她而去，最后为“未相守十几年”错过几十亿。

所以我还是钟情现代资产组合论。他能在很长的时间尺度内创造出风险极低的收益曲线。

有的人配置一只科技股比如NVDA后再配置一只金融股比如BAC，这已经属于分散化。但不仅于此，在这里我讲的宏观一些，让我们看资产的大类：

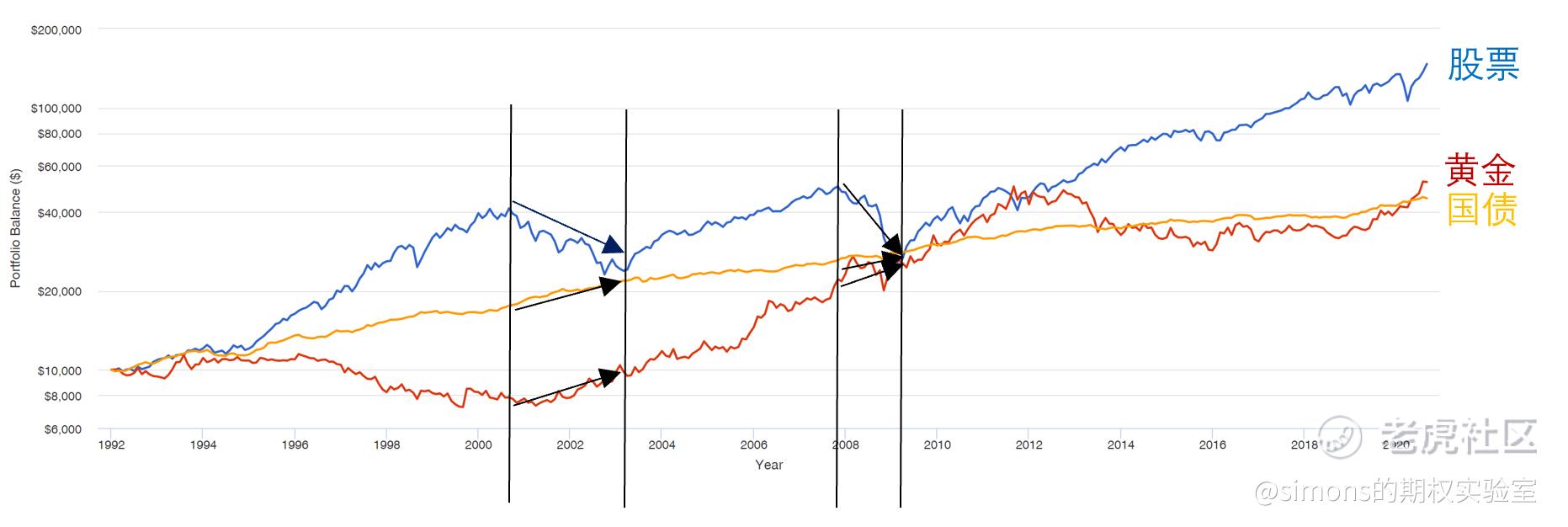
上图是股票（标普）、黄金、国债 三大资产自1992年的收益曲线。股票虽然收益最高，但是其波动性是也是最大的，图中黑色竖线画出了股票的2次大熊市：互联网泡沫和次贷危机。在这2个阶段内，黄金与国债整体是上涨的，体现了负相关性也就是对冲性。

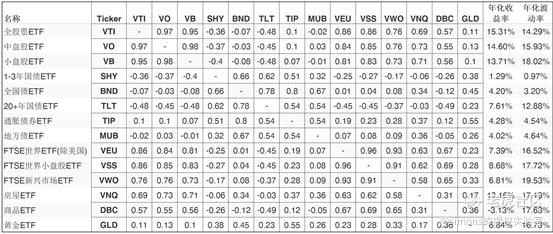
为此我选取了14中最常见的投资各类资产的ETF，他们两两间的相关性如下图。相关性数据在-1~1之间，-1表示完全负相关，1表示完全相关。我们检查一下，跟大盘（VTI）最为负相关的资产为20年国债ETF（TLT），相关性为-0.48。

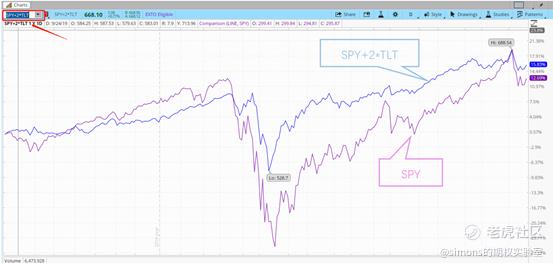
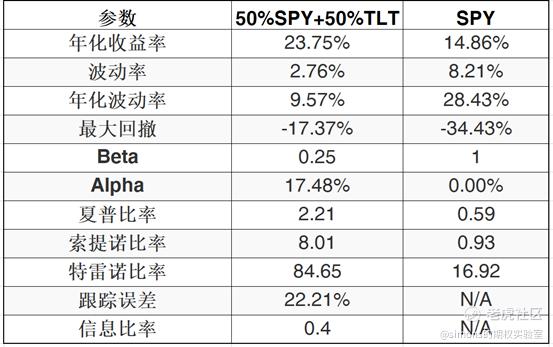
下面我就以TLT与SPY做个简单的资产组合。SPY的价格为340，TLT的价格为165，几乎是2:1的关系。我们假定买入1手SPY并买入2手TLY（也账户内一半的资金买SPY，一半的资金买TLT）。近一年间的表现如图，我们惊奇地发现：SPY+2TLT的组合跑赢了SPY，而且在今年疫情熔断的暴跌中，回撤远远低于SPY。我们运用《读懂你的收益率曲线》学习到的指标来剖析一下2种资产组合，孰优孰劣应该是一目了然的。

惊喜的发现夏普比率达到了惊人的2.0，beta只有0.25，也就是说系统性风险被削弱了1/4。原来把全仓买SPY的头寸分一半出来买TLT会有如此神奇的效果。

关于《现代资产组合论》的前言已经讲完，我们向我们的“圣杯”迈出了坚实的一步。我们学到了分散化（diversified）的概念，其实也接触了对冲（hedge）。关于更有趣的知识，且听下回分解。$债券20+美公债指数ETF-iShares(TLT)$ $标普500ETF(SPY)$ $大盘指数ETF-Vanguard MSCI(VTI)$