塔勒布的书《肥尾效应》的中文版要面试了,感谢中信出版社给我预印本一睹先快。
首先阅读这本书需要一些统计学方面的数学知识,如果大学里学的是理工科方向的话,一般都会学到,只有部分内容涉及到比较高阶的数学,但不影响整本书思想的理解。这本书的核心思想并没有超过过去塔勒布系列书的范围,可以说就是把过去随机漫步的傻瓜黑天鹅和反脆弱等书的思想做了一个比较数理化的阐述。因为作者本身的性格原因,虽然很数理化,依然是得罪人的要命。
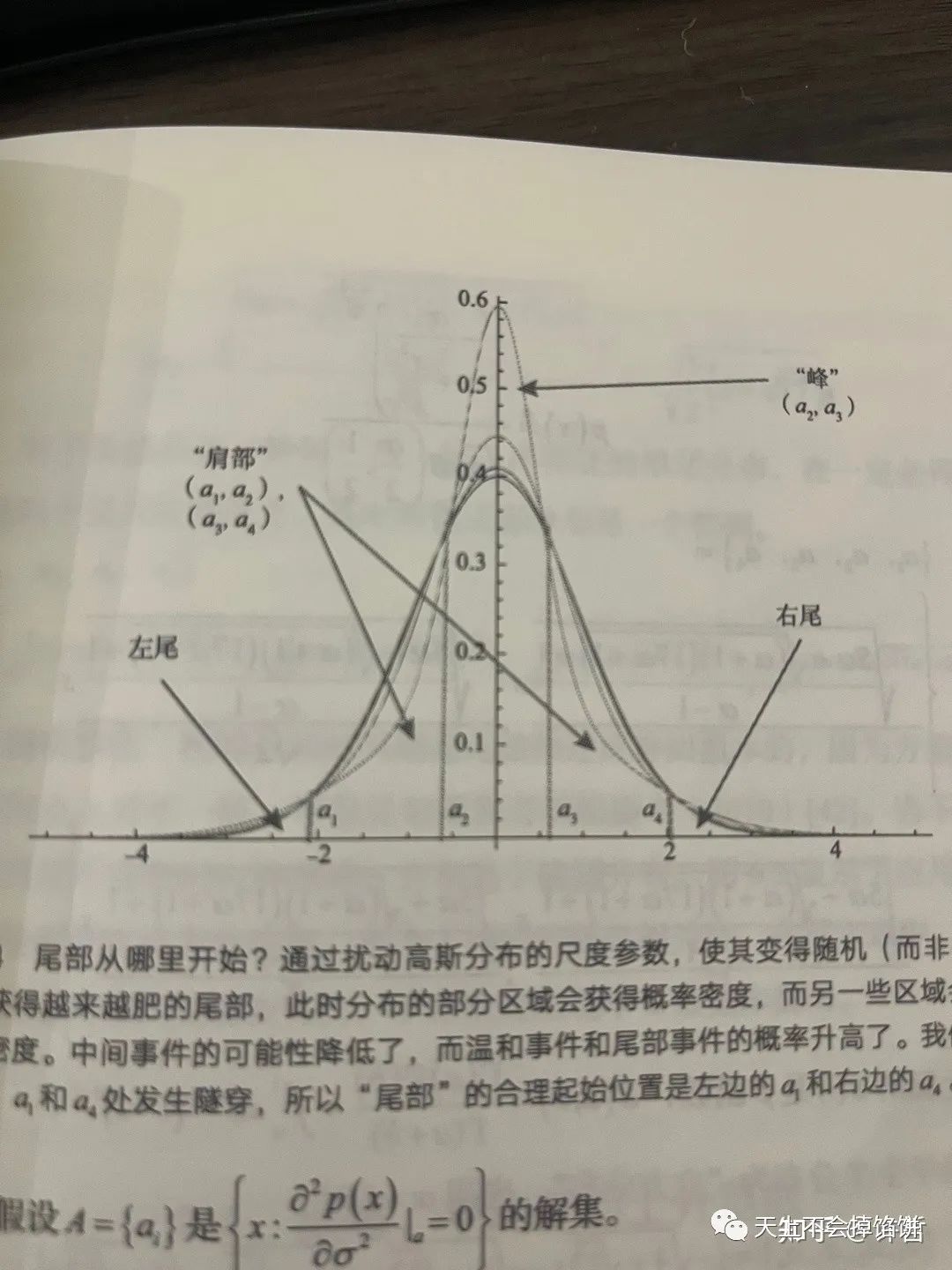
先解释一下肥尾是啥意思,下图是一个很常见的关于概率分布的示意图。中间隆起来的部分我们叫“峰”,两侧是「肩部」和「左尾」和「右尾」。分别代表了不同的分布区间。
比如全国成年男性的身高分布的话,左尾代表了矮于1米的概率,是比较小的,右尾代表了高于2米的人,也是比较小的,大部分人是落在中间,也就是平均身高附近的。左边和右边的尾部都比较薄,这个称为「薄尾」。
正常情况下,这个分布是符合「正态分布」的规律,一系列统计学的结论和成果都是在正态分布的情况下推导得出的。但金融市场并不符合正态分布的薄尾特征,它是肥尾的。也就是发生极端暴涨和暴跌的概率远大于正态分布所描述的那样,于是一系列我们常见的结论和成果并不适用于金融市场。可学界依然不管不顾的做出了很多并没有实用意义的推导和「成果」。也就是下面漫画要讽刺的。
最初步的假设都是不符合实际的话,后面的话都没有意义。书的第十章实证了标普500是符合幂律分布(肥尾的)而不服从正态分布。且作者表示自己统计了4万个证券的收益率,包括了白银原油股票等等品类,没有哪怕一支是符合正态分布的。
那么所有熟悉的手法,基于正态分布的整个体系大厦都轰然倒塌了。
这里自然会讨论到中心极限定律,当N接近无限大的时候,都会趋向于,或者至少可以用正态分布拟合出各种分布来。作者用数理证明的方式论证了收敛到正态的速度会远慢于你爆仓的速度。因为有「吸收壁」效应。一旦肥尾的一边让你爆仓了,那么人生不仅仅只需要暴富一次,一次爆仓也就没有然后了。
所以中心极限定律自然是对的,但主宰市场的依然是肥尾效应,而不是等那个遥遥无期的收敛。
那如果市场是肥尾而非正态的,那么我们能不能构建一个基于肥尾的数学体系大厦呢?很遗憾,这个事情并没有想象中的那么顺利。
我们知道它是肥尾的,但却不知道它具体有多肥。我们知道它过去有多肥,但我们并不知道未来会不会更肥。也就是下面漫画里讽刺的那样。
未来和过去未必有相似性,我们没有办法通过研究过去来规避未来的意外,也就是「黑天鹅」的存在。
如果大坝设计的参照是过去最高水位的记录,那么简单想一想,它所以是记录正是因为它打破了上一个记录,为什么现在这个记录值就是最高不可逾越的呢?如果它对于过去而言是一个意外,那么过去的过去,和过去的未来就没有相似性。这个通常被称为「休谟问题」,书作者认为该思想远早于休谟。面对经济金融领域的肥尾效应,我们能做的只有波普尔的不对称认知,按照塔勒布的说法叫做「揭开概率的面纱」。
这里有一个普遍的误解,如果市场是肥尾且如何肥法无法精确刻画的,甚至过去和未来都不一定具备相似性。那么岂不是我们只知道什么是不对的,不知道该怎么做吗?难道不绝望吗?
塔勒布说:肯定不是没用的,首先能揭露学术界的骗局。(我的大爷哟,您可真是得罪人的行家)
当然这只是一个日常毒舌。
这本书精彩的地方:我们要关注的是 F(X)而不是X。这里的X是资产收益率的随机变量,它是肥尾的但不知道具体有多肥,没有一个精确的函数能刻画,但这并不代表它们对我们产生的效用 F(X) 是彻底让人无助的。也就是下面漫画的内容:我认为市场上涨的概率大,但我选择做空。在亢奋周期下周继续上涨的概率更大,但一旦下跌造成的连环爆仓会让收益大很多。虽然下跌概率小,但乘以它的收益倍数,期望更好。所以投资(机)看到的是效用期望F(X),而不是纠结X的分布怎么刻画。
用索罗斯的话来说就是「关键不是你赌对了还是赌错了,是你对了能赚多少钱,错了会亏多少钱」。
且我们知道了市场不是薄尾而是肥尾的情况下,我们少踩坑(用那些错误的基于正态分布的推导结论),就是一个巨大收获了。且已知肥尾效应存在的情况下,我们是可以利用肥尾的。
既然肥尾是客观存在的,市场真实的情况,那么我们可以用做多四阶矩的方法从肥尾效应中受益。所以肥尾的无法像薄尾那样刻画并不等价于我们无所适从。做多四阶矩就是在意外程度上受益,也就是「反脆弱」的具体手法。当然,这肯定要借助期权类的金融工具。(关于做多四阶矩峰度的具体技术细节参考《动态对冲》)
书的最后部分,塔勒布给出了一种完全不同于BSM的期权定价方法,因为BSM对资产段收益率S有服从正态分布的假设,而本书的结论恰是根本不存在这个假设正确的可能。塔勒布用测度理论给期权定价进行了一种全新的测度积分的表示。仅用了 Call-Put Parity 和无风险套利不存在假设,将看张期权价格对资产S的一阶微分换成了对执行价K的一阶微分,避免了对S分布的假设(不需要资产段收益率分布正态)。
这里仅仅需要K任意多,也就是执行价之间再插入一个执行价不会影响期权的价值。比如100元的看涨期权和101元看张期权多一个100.5的合约,并不影响,这个假设当然是符合现实情况的,完美绕开了对资产收益率分布函数的假设(因为肥尾也没办法确定多肥)。
如果你看过他之前书的系列的话,那么可以说:
随机漫步的傻瓜因为不知道黑天鹅效应而被愚弄,黑天鹅不意味着我们什么都做不了,相反“反脆弱”在这个肥尾的市场下可以更有利。反脆弱就是办法。学界许多聪明的大脑依然死守薄尾无非是教职套利,因为他们不用在真实的市场里躬身入局,有不对称风险。
真实的市场是肥尾的,且我们有办法从中获利,前提是要正视世界的复杂,不要自欺欺人。我想很多市场里的人本能的抗拒肥尾效应是觉得没有抓手,如果世界如此不确定的话。可谁承诺你世界是可理解的呢?为什么整个世界要为你的方便服务呢?去适应世界,别躲在舒适区里不出来然后斥责指出问题的人太极端。




精彩评论