这一期的主要内容我们将介绍期权交易中另一个重要的概念即波动率,标的股票的波动率可以理解为股票价格在指定时间范围内的标准差,表示了股票价格波动的平均幅度大小。
波动率按照分类主要包括历史波动率、隐含波动率、未来波动率。
- 历史波动率(Historical Volatility)衡量特定历史时间段内股票价格的变动幅度,往往通过股票每日回报率的年标准差来计算;
- 隐含波动率(Implied Volatility)是通过期权定价模型计算得到的期权理论价格和市场价格相等时输入定价模型的波动率参数值;
- 未来已实现波动率(Future Volatility)或者未来波动率,是预期未来时间段内的标的资产价格变化的幅度。
隐含波动率(IV)和历史波动率(HV)有一定的关系但又有所区别。
隐含波动率来自于交易者对于市场未来波动率的预期计算所得,而历史波动率来自股票实际历史价格变化数据。一方面,交易者对于期权隐含波动率的估计同短周期的标的历史波动率可能具有较高的相关性;但另一方面,隐含波动率相对历史波动率而言又具有更强的时效性和主观性。
举例来说,在重要基本面比如公司财报发布前,可能观察到HV和IV的分化,尤其当市场对于公司基本面判断无法形成统一意见时,股票交易者对于股票买入持不确定态度,由此观察到股票的历史波动率可能会下降。但是,期权交易者预期在财报公布后可能迎来波动率变化,因此隐含波动率会上涨。而波动率交易的核心则是通过对标的股价未来波动率相对准确地估计以及对于期权隐含波动率的计算进行比较,赚取未来已实现波动率与隐含波动率之间的差价。
针对波动率的计算方法,最普遍采用的方式是利用每日收盘价转换成日收益率而计算出的年化标准差形式,其他计算方法还包括诸如Parkinson估计量、Garman-Klass估计量、Roger-Satchell估计量和Yang-Zhang估计量,不同计算方法在收益率构建上选择不同的价格成分如Parkinson估计量运用最高价/最低价极差为基准的日收益率计算而得,有兴趣的可以进一步了解一下不同的波动率计算方法和差异。
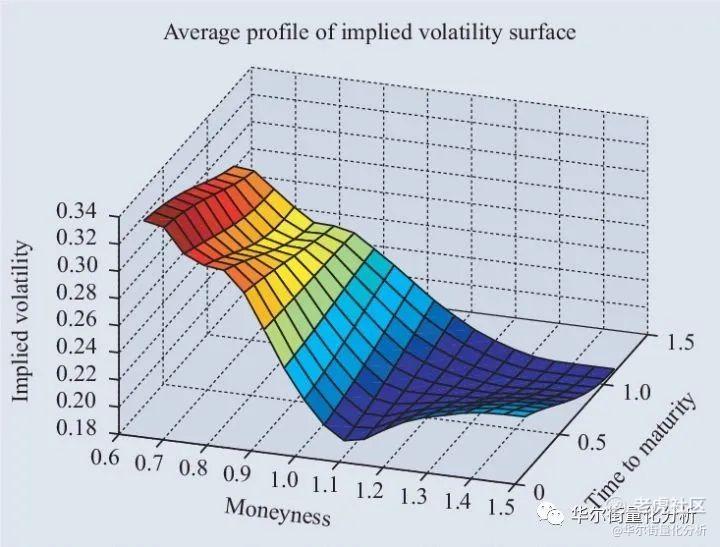
波动率曲面是用来描述隐含波动率结构特征的一个主要方式,描绘了隐含波动率在同行权价格和到期时间所构成的三维坐标空间内的特征曲面。
波动率曲面主要分为期限机构和波动率形态两个部分,其中期限机构是不同期限的期权合约隐含波动率连接成曲线,波动率形态是隐含波动率在标的资产相同到期时间不同行权价格的合约上的分布变化,又通常表现为波动率“微笑”、波动率“正偏斜”和波动率“反偏斜”三种形态。
(来源:https://pic1.zhimg.com/v2-a884d4744c0093d5b5a9557cc5022815_720w.jpg?source=172ae18b)
我们首先来理解一下波动率微笑曲线和偏斜是如何形成的。
由于BS期权定价公式中假设股价运动成对数正态分布,但现实中标的资产收益率更普遍地呈现出尖峰肥尾的特征,即极端值出现的概率比一般正态分布更高。因此BS模型整体低估了到期时期权价值变为深度实值和深度虚值的概率,因而也就低估了深度实值和深度虚值期权价格。在此基础上,根据交易者以及不同标的资产市场对于价外期权和价内期权的相对需求程度高低,波动率曲线又会分别呈现出正偏斜、微笑和反偏斜三种形态——
第一种如图2所示,波动率正偏斜表明相同到期日的合约中,行权价越高隐含波动率也会越高,表明市场交易者对于标的的价外看涨期权和价内看跌期权的需求要高于价外看跌期权和价内看涨期权,因此价外看涨期权的实际价格往往高于BS模型理论价值。波动率“正偏斜”往往出现在大宗商品市场和农产品市场,因为这些标的市场往往具有较高的上涨风险,期权工具往往被用于作为对冲和风险管理的一种手段,商品的买家愿意付出“额外的溢价”防范价格上涨风险。
第二种是波动率微笑曲线,表明深度虚值期权和深度实值期权的波动率高于平值期权,通常表现在外汇期权市场,由于外汇下注的是两个货币对及其政治经济体发展情况,往往不会存在单边看涨或者看跌偏好。
(来源:https://th.bing.com/th/id/R.3179a79be7a810631d940239c37d2da2?rik=iKdmO6%2bYxmbVtg&riu=http%3a%2f%2fwww.theoptionsguide.com%2fimages%2fforward-vertical-volatility-skew.gif&ehk=bKiXzxVQC33NruyiVSyaMdBZ4et6xQYda%2bkHb495vLs%3d&risl=&pid=ImgRaw&r=0)
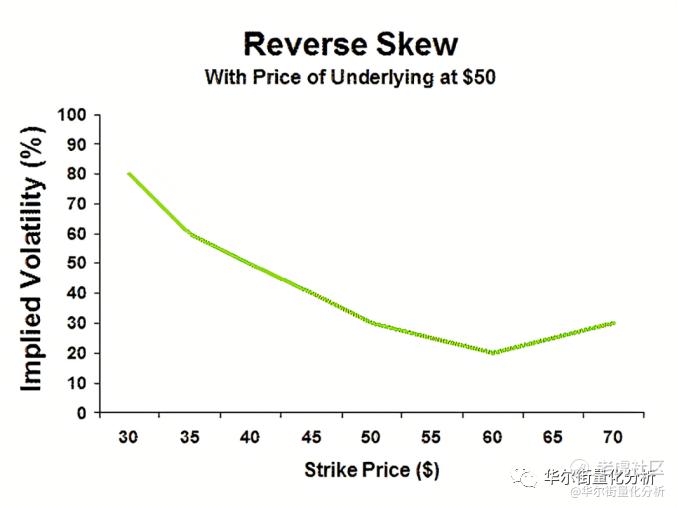
第三种是波动率反偏斜,通常表现在股票期权市场,表明交易者对于标的的价外看跌期权和价内看涨期权的需求要高于价内看跌期权和价外看涨期权。股票交易者往往倾向于买入并持有股票,相较于付出更多的溢价防范价格上涨的风险,更愿意付出更多的溢价防范价格下跌回撤的风险,由此观察到价外看跌期权的价格高于其期权定价模型的理论值。
(来源:https://www.theoptionsguide.com/images/reverse-vertical-volatility-skew.gif)
波动率期限结构 是衡量期权隐含波动率水平的另一个重要指标,反映了期权合约 在不同到期时间的隐含波动率水平以及远期波动率与近期波动率的关系 。由于期限结构斜率变化反映了市场近期与远期之间波动率水平差异。一般情况下,波动率期限结构倾向于上偏斜,即近月的隐含波动率要小于远月,但随着时间增长隐含波动率的变化幅度会衰减。然而当行情出现大幅的波动时,可能会引起近月隐含波动率高于远月,观察到波动率期限结构向下偏斜。根据隐含波动率近期与远期价差大小或者波动率曲面结构的特征分布,可以衍生出一系列波动率交易策略。
波动率预测被广泛应用于 delta 中性期权交易 ,通过预期未来标的价格的已实现波动率与隐含波动率之间的价差来获得收益。
比如以平值跨式期权策略为例,策略多头通过同时买入相同行权价格、到期日、相同数量的平值看涨期权和看跌期权实现 delta 中性的基础上,通过基本面或者交易系统信号分析,如果预期标的股价的未来已实现波动率将大于隐含波动率,则可获得 gamma 收益,即预期 gamma 变动的收益大于 theta 衰减的损失。反之,策略空头会同时卖出相同行权价格、相同到期日、相同数量的平值看涨和平值看跌期权,通过预期标的资产的未来波动率将在一定的窄幅区间内波动,导致已实现波动率小于隐含波动率,则可获得做空波动率的 theta 收益,卖方预期 theta 盈利覆盖 delta/gamma 变动的损失。当然平值跨式期权还只是波动率交易的一个小策略,围绕波动率交易还有更多复杂多元的策略可以探索。
波动率交易是期权交易中的 「 皇冠 」 ,也可以认为是期权交易最重要的一个方面,这一期关于期权波动率的基础知识介绍到这里,我们回顾了不同期权波动率概念的定义、隐含波动率的期限结构特征以及波动率在期权交易中的主要应用。
感谢大家的关注和阅读,欢迎评论区留言讨论!
〓 End 〓
撰文:Joey // 指导:Evan // 排版:Olivia









精彩评论