最近在看华泰金工的多因子和人工智能两个系列的研报(强烈推荐),并在逐步复现。多因子系列的第六篇波动率类因子里有两类特质波动率,其中第二类特质波动率是由近 n个月内 Fama-French 三因子回归残差的标准差构成,因子分析效果比较理想,并在人工智能系列里继续作为特征使用。这个系列的因子实现上稍微有点复杂,我在网上没有看到跟华泰金工思路一样且实现正确的代码,所以我觉得把我的实现分享出来是有一定价值的。
波动率类因子的基本原理是,如果某只股票在过去一段时间的波动率明显高于同类型股票的平均水平,则该股票可能是近期资金多空角逐比较激烈的战场,一般来说,个股波动率高从统计意义上讲是负向指标。
特质波动率因子将股票的系统风险与公司层面的特质风险剥离开来,一般可以简单基于CAPM 模型计算股票特质波动率,即为过去一段时间内个股日收益率序列对市场组合(报告里采用中证全指,我们为了节省时间用的沪深300)日收益率序列进行一元线性回归的残差的标准差(剔除停牌的交易日)。
特质波动率的度量方式有许多种,可以使用 CAPM回归残差序列的标准差进行计算,也可以更精细地使用 Fama-French三因子模型的回归残差序列的标准差进行计算。三因子与 CAPM 比较,相当于新引入了规模因子和账面市值比因子,本文实现的就是这类因子。
Fama-French三因子模型残差波动率因子即为过去一段时间内个股日收益率序列对市场组合(我们这里采用中证全指)日收益率序列、规模因子日收益率序列、账面市值比因子日收益率序列进行多元线性回归的残差的标准差(剔除停牌的交易日)。其中,规模(或账面市值比)因子日收益率的计算方法为前一日市值(或 PB)排后 30%的股票的本日收益均值减去前一日市值(或 PB)排前 30%的股票的本日收益均值。
个人基本复现了华泰的多因子分析框架,下面以沪深300为分析对象,时间范围为2008年1月1日到2018年12月31日,每个月末取因子截面,跟下个月的收益做关联,得出因子的IC分析、t检验和分五层测试的结果如下:
IC分析结果:
结果表明随着波动率计算周期的增加,因子效果逐渐减弱,前三个因子的IC分析结果较理想,ff_rsd_std_1m表现最佳。
t检验结果:
结果表明随着波动率计算周期的增加,因子收益率依次减少,但t值都不显著,ff_rsd_std_1m表现最佳。
分层测试结果(五层):
上表展示的是每个因子对应的每层相对于沪深300指数的年化超额收益,可以看出各个因子的不同层次的超额收益都表现出了明显的单调递减,ff_rsd_std_1m表现最佳。
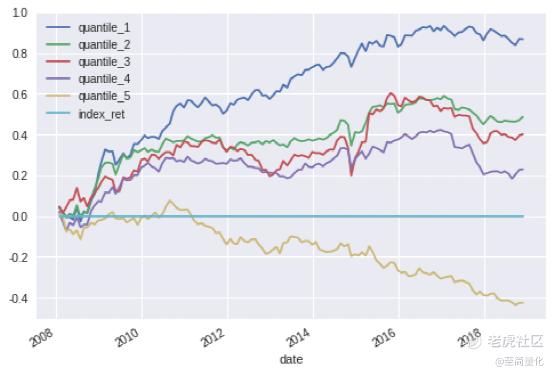
下图是ff_rsd_std_1m因子各层的累计超额收益曲线:
总结一下,整体来看Fama-French三因子模型残差波动率因子选股效果不错,而且选取的波动率周期越短得到的因子效果越好。
整个分析框架代码较多,此处仅附上ff三因子残差波动率因子的主要代码(基于聚宽平台):
#获取ff三因子残差波动率因子
def query_ht_factor(securities: list, watch_date: str) -> pd.DataFrame:
'''华泰证券多因子'''
import warnings
warnings.filterwarnings("ignore")
data=pd.DataFrame(index=securities)
#获取最近240个交易日
trade_days=list(get_trade_days(end_date=watch_date, count=240))
SMB=pd.Series()
HML=pd.Series()
RM=pd.Series()
R=pd.DataFrame()
for i in trade_days:
stock = get_index_stocks(index,date=i)
stock_close=get_price(stock, count = 1, end_date=i, frequency='daily', fields=['pre_close','close'])
mkt_close=get_price(index, count = 1, end_date=i, frequency='daily', fields=['pre_close','close'])
#股票收益率
stock_chg = (stock_close['close']-stock_close['pre_close'])/stock_close['pre_close']
#市场收益率,famafrench三因子之一,假设无风险利率为0
mkt_chg = (mkt_close['close']-mkt_close['pre_close'])/mkt_close['pre_close']
q = query(valuation.code,valuation.market_cap,valuation.pb_ratio).filter(valuation.code.in_(stock))
temp = get_fundamentals(q, i)
#将市值的单位从亿元转为元
temp['market_cap']=temp['market_cap']*100000000
#将pb转为bp
temp['bp'] = 1/temp['pb_ratio']
temp.index = temp['code']
del temp['code']
LoS = len(stock)
#将当天的股票按bp排序,分别选前30%和后30%代表低和高bp的股票
L=temp['bp'].sort_values()[:int(LoS*0.3)].index
H=temp['bp'].sort_values()[int(LoS-LoS*0.3):].index
#famafrech三因子之一,代表低bp股票对高bp股票的超额收益
HML = HML.append(stock_chg[H].mean(axis=1)-stock_chg[L].mean(axis=1))
S=temp['market_cap'].sort_values()[:int(LoS*0.3)].index
B=temp['market_cap'].sort_values()[int(LoS-LoS*0.3):].index
#famafrech三因子之一,代表低市值股票对高市值股票的超额收益
SMB = SMB.append(stock_chg[S].mean(axis=1)-stock_chg[B].mean(axis=1))
RM = RM.append(mkt_chg)
R = R.append(stock_chg)
#求因子的值
#整合三因子
X=pd.concat([RM, SMB,HML], axis=1)
#加入截距项
X=sm.add_constant(X)
Y=R
#将股票收益率对三因子做ols回归
ffm=sm.OLS(Y,X)
results = ffm.fit()
#用线性回归结果预测股票收益率
y_fitted = results.fittedvalues
#计算残差
residuals=Y-y_fitted #保存残差(有正有负)
residuals = residuals.loc[:, securities]
#计算过去1、3、6、12个月的ff三因子残差波动率
data['ff_rsd_std_1m']=np.mean(residuals.iloc[-20:],axis=0)
data['ff_rsd_std_3m']=np.mean(residuals.iloc[-60:],axis=0)
data['ff_rsd_std_6m']=np.mean(residuals.iloc[-120:],axis=0)
data['ff_rsd_std_12m']=np.mean(residuals.iloc[-240:],axis=0)
# 辅助项,市值和行业,用来做市值和行业中性化
ind_cap = IndusrtyMktcap(securities, watch_date)
data = pd.concat([data, ind_cap], axis=1)
return data



精彩评论