怎样取得成功?成功人士的秘诀又是什么?这些问题共同构成了一门经久不衰的学问——成功学。
描写成功人士的文章和著作,都有着相似的叙事逻辑,即他们的成就都归功于出类拔萃的个人特征,如天赋、智商、情商、才能或是精神品格。这种设定不仅是大部分成功学的基础,也影响着社会资源的分配方式。
于是就有一种自然而然的假设:最成功的人,往往也是最有能力的。
很少有人去验证该假设是否正确,因为它本身就带有事后偏见(Hindsight Bias),是通过一种事后决定论的机制来寻找成功的“原因”。
事实上,是人们需要这些原因。因为只有这样,才能把一个个随机选择和意外因素串联成令人信服且合乎逻辑的故事,而故事,通常更受欢迎。
在这种相对主流的成功叙事中,运气鲜少被提及或往往被忽略,因为它的存在可能会削弱故事主角的能力,不利于人物形象的塑造。
不过,这只是其中的一面。如果以财富作为成功的一个标准,在另一面,则写有不少“幸运儿”的故事。
在移动互联网时代,某人因为一句话、一个动作、一张照片或一个视频全网走红的事件屡见不鲜,而且可以说是当下“最容易”且常见的一种成功方式。巨大的流量本身就会产生经济效益和财富流动,所以许多爆红事件总会伴随着这样一些网络流行句式:“命运的齿轮开始转动了”,“泼天的富贵轮到____了”。
网红现象所带来的造富神话,显然不同于前面提到的那种成功叙事,也无法用那样的逻辑和假设来解释。对于巴菲特的成功,很少有人会说他只是“运气好”,而对于网红的成功,倾向于认为是“走运”的却是大多数。
那么,在像巴菲特这样成功的人身上,是否也存在“运气”的成分?要讨论这个问题而不陷入“宿命论”的窠臼,就需要从科学的角度去探究“运气”的影响。
先来看前面的假设会有什么问题。
社会许多层面的资源分配都遵循着一种众所周知的模式——80/20定律(也称为幂律或帕累托定律),80%的资源由20%的人所拥有。其中,财富的分配是最具争议的问题之一。
用智商、才能或努力等因素来解释财富分配的不均的问题就在于:虽然财富分配遵循幂律,但解释因素的分布却通常呈正态分布。
以智商为例,平均智商为100,智商在平均水平上下一定范围内发生偏离最普遍的情况,但几乎没有人的智商高出平均值十倍或是一百倍。如果以工作时长衡量努力程度也是如此,工作时长大于或小于平均时长的情况都有可能,但不会出现工作时长比其他人多出数十亿倍的情况。
在此基础上,几个意大利学者用数学模型对运气进行了量化。
在这篇题为《Talent vs Luck: the role of randomness in success and failure》的论文中,意大利物理学家Alessandro Pluchino和Andrea Raspisarda与经济学家Alessio Biondo合作,共同回答了一个问题:运气在成功中扮演了多大的角色?
研究方法和过程都很简单(甚至是有些过于简单,这一点稍后会讲到)。
研究者构建了一个物理和数学相结合的模拟模型,称为“才能与运气”(Talent vs Luck,TvL)模型。
1000个(N=1000)具有不同程度才能(智力、技能等)的个体随机分布在一个正方形的二维空间里,每个人拥有相同数量的资本(C=C(0),∀i = 1, ..., N),表示成功/财富的起始水平。
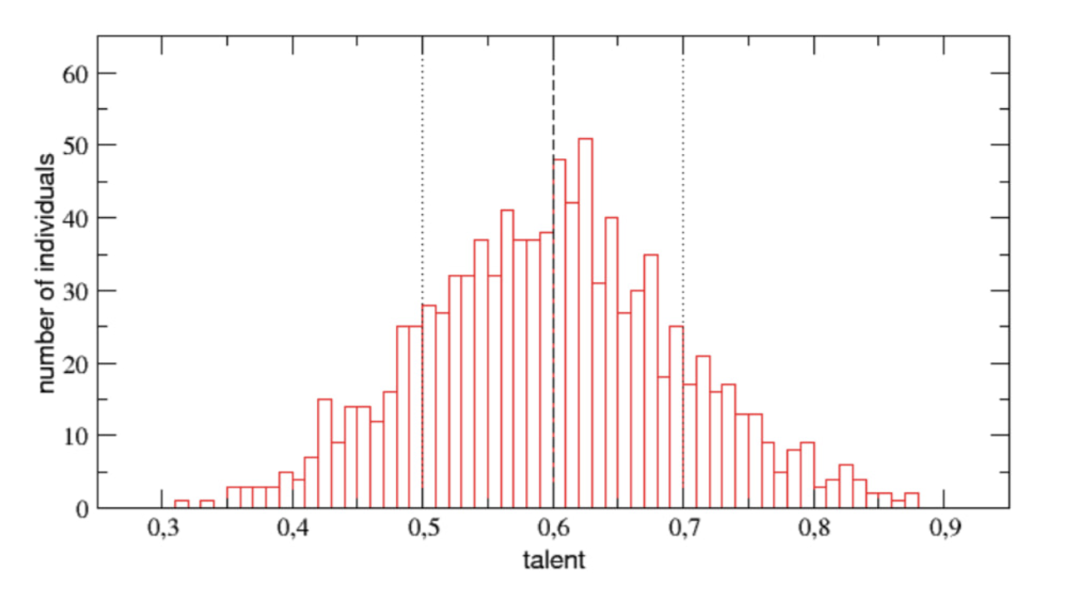
每个人都有一个才能参数T,该参数正态分布在区间[0,1]内,给定均值m=0.6,标准差𝜎=0.1,且才能不会随着时间或模拟而改变。
△1000个人的才能分布情况
接着是模拟的过程。
每个人都会工作四十年,与现实中20岁到60岁的职业生涯时间跨度相对应。
每个人都被许多均匀分布的随机移动事件包围:绿色圆点表示幸运,红色圆点表示不幸。
每个人每六个月就会遇到一次幸运或不幸的事件。如果没有遇到任何事件,则财富保持不变。
遇到有利事件,个体以与自身才能T成正比的概率获得财富/成功加倍,即
rand[0,1]
如果遭遇不幸,则损失一半财富。
C(t) = C(t − 1)/2
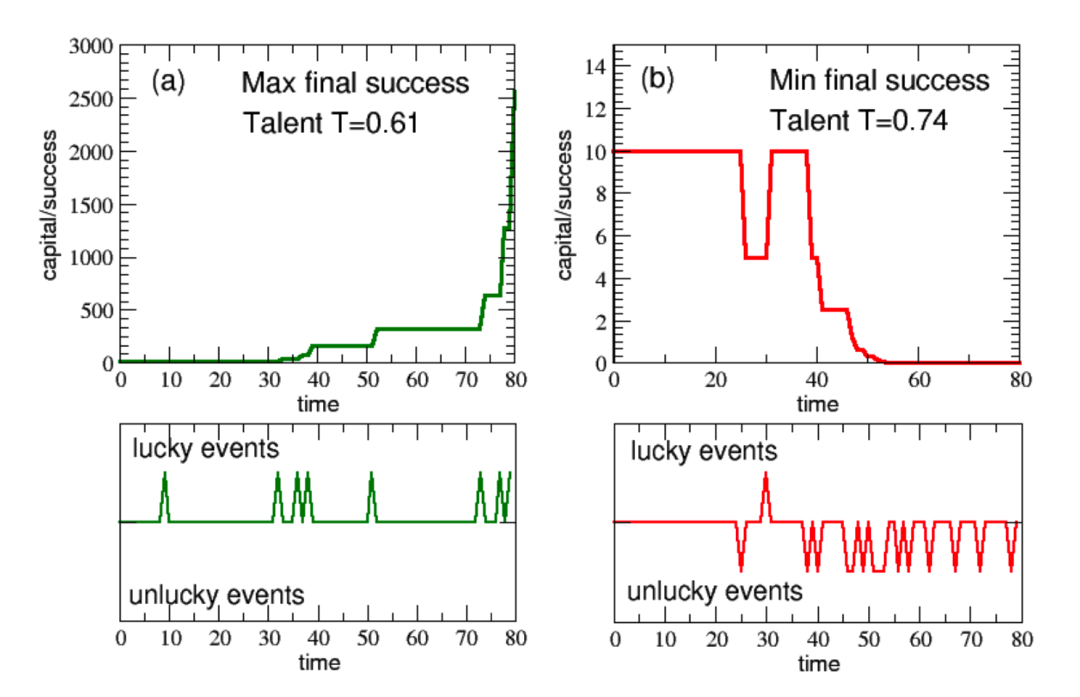
△左图显示了一位才能普通但极其幸运的人取得了极大的成功。右图显示了一位更有才能但极其不幸的人陷入了困境。
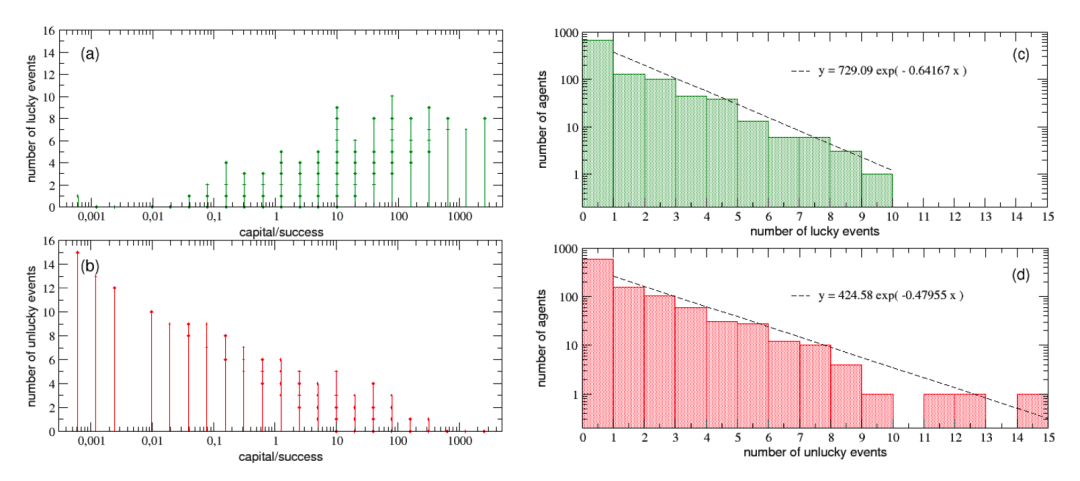
△幸运事件(a)和不幸事件(b)作为个体财富/成功的函数
根据模拟的结果,研究人员发现,模型中的财富分配与现实中的幂律分配相吻合,然而,最成功的人并不是才能最高的人,才能最高的人也不是最成功的人。同时,运气对个人的成功产生了巨大的影响,并表现出很高的相关性。
一个才能一般但运气高于平均水平的人,比一个才能极高但运气不佳的人表现更好。如此一来,表现最好的就是那些运气最好,且才能略高于平均水平的人。
所以论文得出的结论是,最成功的人也是最幸运的人:成功和运气密切相关。作者还总结道:“即使才华横溢,在厄运面前也会变得毫无用处。”
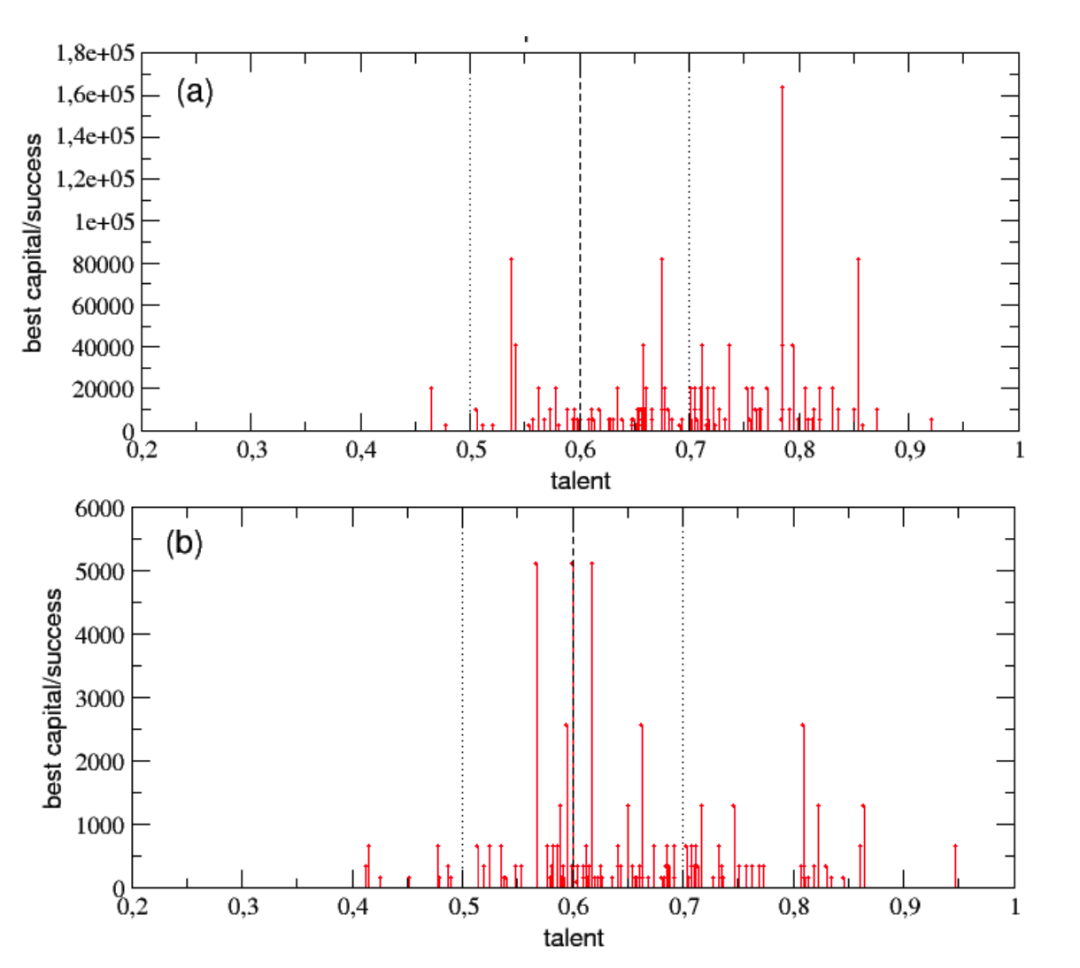
此外,研究者进一步模拟了不同机遇环境下的成功情况。
在充满机遇的环境下,一些才能处于中上水平的人都取得了高于平均水平的成功。部分才能中上的人取得了很高的成功。而在缺乏机遇的环境下,几乎没有人取得成功。其中只有大约18个人的最终财富比初始值高。
这篇论文为我们提供了一个量化运气的有趣视角,但它的问题也是显而易见的。
论文提供的支持该模型的证据缺乏说服力,现实世界和模型之间唯一的关联是模拟结果遵循80/20法则。
即便忽略有力证据的缺失,我们在之前的推文中讲相关性与因果性问题的时候也提到过,与数据拟合良好的模型并不一定能很好地概括实际的情况。(👉🏻《准确率超过90%的预测模型为什么不靠谱?》)
不过,从科学的角度去理解运气是有意义的。很多时候运气都因其不可预测和不确定的特点被视为一种玄学或不可知论,而这种特性其实就是随机性,这是我们已知的未知。
随机性的问题我们之前也讨论过,以投资为例,同样的市场,不同的策略决定了投资性质的不同,有的人玩的是概率游戏,有的人则是玩成了纯随机的抽奖游戏。(👉🏻《为什么好的量化策略一定赚钱?》)
正如物理学家和博弈理论家Richard Arnold Epstein所说:“如果一项活动既靠实力,又靠运气,那么没人能保证你一定会赢。”但是,明白为什么输,才有可能赢,明白为什么赢,才可能赢得更多。所以他也说过:“宁愿聪明地输,也不要糊涂地赢。”
好运不会平等的降临在所有人头上,但无论是论文中的结论还是现实情况都表明,当好运出现时,只有具有一定能力的人才能抓住并利用它取得成功。
了解随机性的存在,明白事物运作的规律,可以让我们按照正确的方法做好每一个决定。这样一来,对于任何可能的结果,都能坦然接受,也能更加客观地分析个中原因,理智地做出下一步决策。
毕竟,在投资中,成功并不是只由一次结果决定。
Fun facts:
这篇论文获得过“搞笑诺贝尔奖”(Ig Nobel Prizes,名称来自Ignoble和Nobel Prize的组合)。该奖项是对诺贝尔奖的戏仿,以表彰那些“乍看令人发笑,然后让人思考”的研究。
该奖项创立于1991年,每年九月中旬(在真正诺奖的前两周)举行颁奖典礼,举办地点最初在MIT,1994年后移至哈佛大学桑德斯剧院并持续多年,2024年又返回MIT举行。评委和颁奖者大多时候是真正的诺奖得主。搞笑诺贝尔奖获奖者会发表演讲,还会得到“高额”的奖金,一张面额100万亿的——津巴布韦纸币(相当于人民币2.5元)。
2000 年,Sir Andre Geim因利用磁力使青蛙悬浮而获得搞笑诺贝尔奖,2010年,因其对石墨烯电磁特性的研究而荣获诺贝尔物理学奖。到目前为止,他是唯一一位同时获得搞笑诺贝尔奖和诺贝尔奖的人。
下面是2024年“搞笑诺贝尔奖”的获奖研究:
解剖学奖:发现南半球的人头发旋涡相比于北半球更有可能呈逆时针方向螺旋。
生物学奖:发现在一只站在牛背上的猫旁边反复引爆纸袋,会导致牛产奶量减少。
化学奖:利用色谱法分离醉酒和清醒的蠕虫。
植物学奖:发现某些植物模仿附近塑料植物的叶子形状,并得出“植物视觉”结论。
人口统计学奖:发现超级百岁老人和极端高龄记录往往来自那些没有出生证明、文书错误严重、养老金欺诈和寿命较短的地区。
医学奖:发现引起痛苦副作用的假药比不会引起痛苦副作用的假药更有效。
和平奖:将活鸽子安置在导弹内部以指引导弹飞行路径的实验研究。
物理学奖:演示和解释死鳟鱼的游泳能力。
生理学奖:发现几种哺乳动物可以通过肛门呼吸。
概率学:一个由50名研究人员组成的团队进行了 350757 次实验,发现抛硬币时,更有可能落在与开始时相同的一面。





精彩评论