概率游戏——浅谈投资的本质

早前在老虎社区的访谈中【实盘面对面】FrankAllin：概率思维看期权交易实战方法，我简单分享了个人期权交易的基本框架，并将投资视为一种概率游戏。

在这里，我想借这个概念，进一步展开谈谈对投资的理解，以及如何构建适合自己的投资体系。

先谈谈我所理解的投资的本质是什么。

• 什么是投资？

根据维基百科的定义，"Investment is traditionally defined as the "commitment of resources to achieve later benefits". If an investment involves money, then it can be defined as a "commitment of money to receive more money later".

实际上，当我们谈论投资时，一般都是指金钱的投资。

在这个前提下，投资可以简单地理解为： “放弃货币的现时使用价值，以获得未来的使用价值。”

因而，只要我们当下没有把持有的货币消费掉，那么我们就是在进行投资。

区别在于，我们选择不同的方式来实现货币的未来价值。

比如，将钱投入到实体经济（如开厂或开店）以期获得未来利润，这属于实体投资；而将钱投资到金融资产（如股票、债券、银行存款），则是金融投资。

• 投资里的变量

在投资中，我们关注的是如何将投入的本金和时间转化为未来的货币价值的过程。

未来的货币价值应当是关乎本金和时间的函数：

F=f(P,t)

其中，F代表未来的货币价值，P为现时价值，t为时间。

如果在相同的本金和时间条件下，是什么导致了未来货币价值的差异呢？通常情况下，我们会引入一个收益率（r）的变量，将公式变为： 

F=P+r×P×t

如果P和t都是固定的，那么影响投资结果的变量就是r。

• r应该是什么？

我们通常讨论的r，往往是一个后验的概念，即通过已实现的收益来倒推收益率，并将其视为一个自变量。

这会产生误导，因为这个后验的r掩盖了背后的随机性和不确定性。

站在未来的角度来看过去，已实现的收益率是确定的；但从现时的角度看未来，收益率是不确定的。

比如，当前以100元的现价买入的一只股票，一年后的股价从当前这个节点来看，是不确定的，它可能变成120元，也可能变成80元。

这种可能性，就是概率（probability）。

即便是所谓的无风险资产，其约定收益的实现概率也只是接近100%，而不是绝对的100%。比如存款，在极端情况下也可能遭受损失。

对于固定收益资产（债券、存单、贷款等），即使合同约定了固定收益率，到期时仍然存在一定的概率，因对手方违约或其他不可控原因而无法实现约定收益。

r应当被视为一个随机变量。

• 重新思考收益率的意义

设想一个情景：

玩一个掷硬币游戏，下注100元，有50%的概率（硬币正面朝上）赢得100元，50%（硬币反面朝上）的概率输掉本金100元。

如果你第一次运气不错，掷到了正面朝上，赢得了100元。

那么你的收益率是多少？一般人大概会回答100%。

但从概率的角度来看，这个结果是后验的。

假设这个游戏重复玩100次呢？你的收益会是多少？

根据概率论，重复博弈后的结果会遵从大数定律，平均收益率将趋近于0。

仅仅关注后验的收益率是没有意义的，更重要的是要辨别，这个收益率背后隐藏的概率结构和风险，才是有意义的。

风险是什么？

风险也是一种概率，即为本金遭受损失的可能性。管控风险，本质上就是管控投资本金损失的概率。

• 除了概率，还有什么？

还有赔率（odds）。

人们常说：“高风险高收益”。

从概率的角度理解，这意味着赔率必须与概率相匹配。

对于小概率盈利而大概率亏损的游戏，人们通常期望更高的回报；而对于盈利概率高的游戏，市场博弈后的均衡会导致较低的赔率。

例如，低风险的国债或货币基金，盈利概率高，赔率相应较低；而高风险的股票、期货和PE，盈利概率低，赔率相对较高。

赔率与概率匹配，是市场博弈后均衡的结果。

盈利概率低且赔率低的市场是否存在？确实存在，但不会持久。当市场上的“傻子”被淘汰完后，这样的市场也将消失。

在投资这个概率游戏中，我们不仅仅要关注概率，赔率同样重要。

只有在概率和赔率都合适的情况下，投资才值得进行。

• 概率和赔率的游戏

所有的投资都可以抽象为概率和赔率的游戏。

只是由于选择的不同的投资方式和载体，改变了我们所面对的概率和赔率的结构。

譬如，

• 某存单：1年后有99.99%的概率能获得2%的收益，有0.01%的概率无法取出本金；

• 某信用债：1年后有90%的概率能获得5%的收益，有10%的概率损失全部本金；

• 某股票：1年后有10%的概率获得50%收益，30%的概率获得10%收益，30%的概率亏损10%，10%的概率亏损20%；

• 某VC项目：1年后有5%的概率获得300%收益，10%的概率获得100%收益，85%的概率损失全部本金。

这些资产，哪个值得投资？哪些是不值得投资的？

相信大家都很容易算出来，通过概率和赔率，很容易得到收益的数学期望，即EV（expected value）。

常玩德州扑克的朋友应该都知道EV的概念。

在德州扑克中，一局的输赢代表不了一个牌手的真正水平，长期的正EV才是关键的。

为了取得正EV，优秀的玩家会在每次下注时，评估并管控好赢牌的概率和赔率。

投资也是如此。

投资不能只看后验的收益率，更多是一个关于概率与赔率的博弈。

我们需要理解投资背后的概率结构，在每一次下注中，管控好盈利的概率和赔率，才能在长期中实现正EV。

—————————————————————人为的分割线 ———————————————————

图片

那么，如果我们能够有效地管理 r 的概率和赔率，是否就能持续获得正的期望值（EV）呢？

答案是：可以，但还不够。

相信从事投资的朋友们，都经历过一段顺风顺水的时期——收益不错，仿佛无论怎么操作都能获利。我也不例外。

刚开始做期权卖方时，自认为选择了高概率的策略，长期来看可以持续获利。在短期内，甚至将账户收益翻倍。

然而，一天，突如其来的“黑天鹅”事件打破了这种平衡，超预期的市场波动让我持有的期权空头仓位蒙受巨大损失，几乎濒临爆仓。之前积累的利润，一夜之间化为乌有。

为什么会这样？

明明我的操作模式下，胜率和赔率都适宜，理论上应有正的期望值，为什么还会巨亏呢？

当时的我还不懂得，什么是“遍历性”。

• 什么是遍历性

遍历性（Ergodicity）原本是统计力学中的一个概念，指的是统计结果在时间和空间上的一致性，表现为时间均值等于空间均值。

为了更好地理解这个概念，我们用掷硬币的例子来说明。

同时掷一百个相同的硬币，统计其头像面朝上的均值，再用同一个硬币掷一百次，统计其平均值。如果这两个均值相等，那么这个过程就具有遍历性。

显然，对于掷硬币这种典型的伯努利试验来说，它是具有遍历性的。

相反，不具备遍历性的一个典型例子是俄罗斯转盘。

假设一把左轮手枪弹夹里有一发子弹，其他五个弹夹是空的。如果六个人轮流用这把手枪对着自己的头部扣动扳机，空弹的人将获得100万美金的奖励，而被真子弹击中的人将失去一切。很容易计算出，每个人有5/6的概率获得100万美金，有1/6的概率丢失性命。那么，如果是同一个人连续玩六次这个游戏呢？是的，他100%会丧命。

显然，在俄罗斯转盘这个游戏中，空间均值不等于时间均值，因此它不具备遍历性。

为什么会这样？因为这个游戏中有一个退出机制，一旦触碰到某个概率点，你就会被强制退出，离开这个游戏。换句话说，你无法继续遍历这个游戏的所有概率了，因为在中途就已出局。

在投资交易中，也存在这种退出机制，那就是爆仓。一旦爆仓，就意味着失去所有本金，彻底失去了继续参与游戏的权利。这时，后续的概率和赔率对你来说已经毫无意义。

• 集合概率与时间概率

塔勒布（Telab）在《Skin in the Game》一书中通过一个例子来解释遍历性：

假设有100个赌徒各自带着1万美金去赌场赌一个游戏，这个游戏有人能赢，有人会亏，也有人会爆仓。根据他们的平均收益和亏损，可以大致估算出这个游戏的概率和赔率。如果其中第10个赌徒爆仓了（输光了本金），并不会影响第11个及其他赌徒的结果，他们的概率相互之间是独立的。假设这个游戏的爆仓概率是1%，那么如果一直重复这个游戏，大概会有1%的赌徒爆仓。换个场景，如果是同一个赌徒带着这100万去赌场玩这个游戏，重复玩100次呢？按照1%的爆仓率来说，只要他赌的次数足够多，爆仓就几乎是必然的。

对于第一个场景，这个1%的爆仓率是集合概率。这100个赌徒参与游戏的动作是独立且并行的，对于系统而言，个别赌徒的爆仓不会影响其他参与者的结果。

而第二个场景则是时间概率。

同一个人重复参与博弈的过程是串行的，任意次博弈的结果都会影响后续，一旦在某个节点上爆仓，他就失去了继续参与游戏的机会。

从系统的角度看，集合概率具有遍历性。系统内某些人的出局不会影响整个系统的运行。而对于时间概率而言，如果这个游戏有退出机制，一旦出局就失去了后续参与权，那就是缺乏遍历性的。

回到金融市场，对于市场的所有参与者而言，整个集体面对的是集合概率。市场每天都有参与者爆仓和爆赚，每天都会淘汰一部分人。但这些人的淘汰并不会影响市场的正常运行。

图片

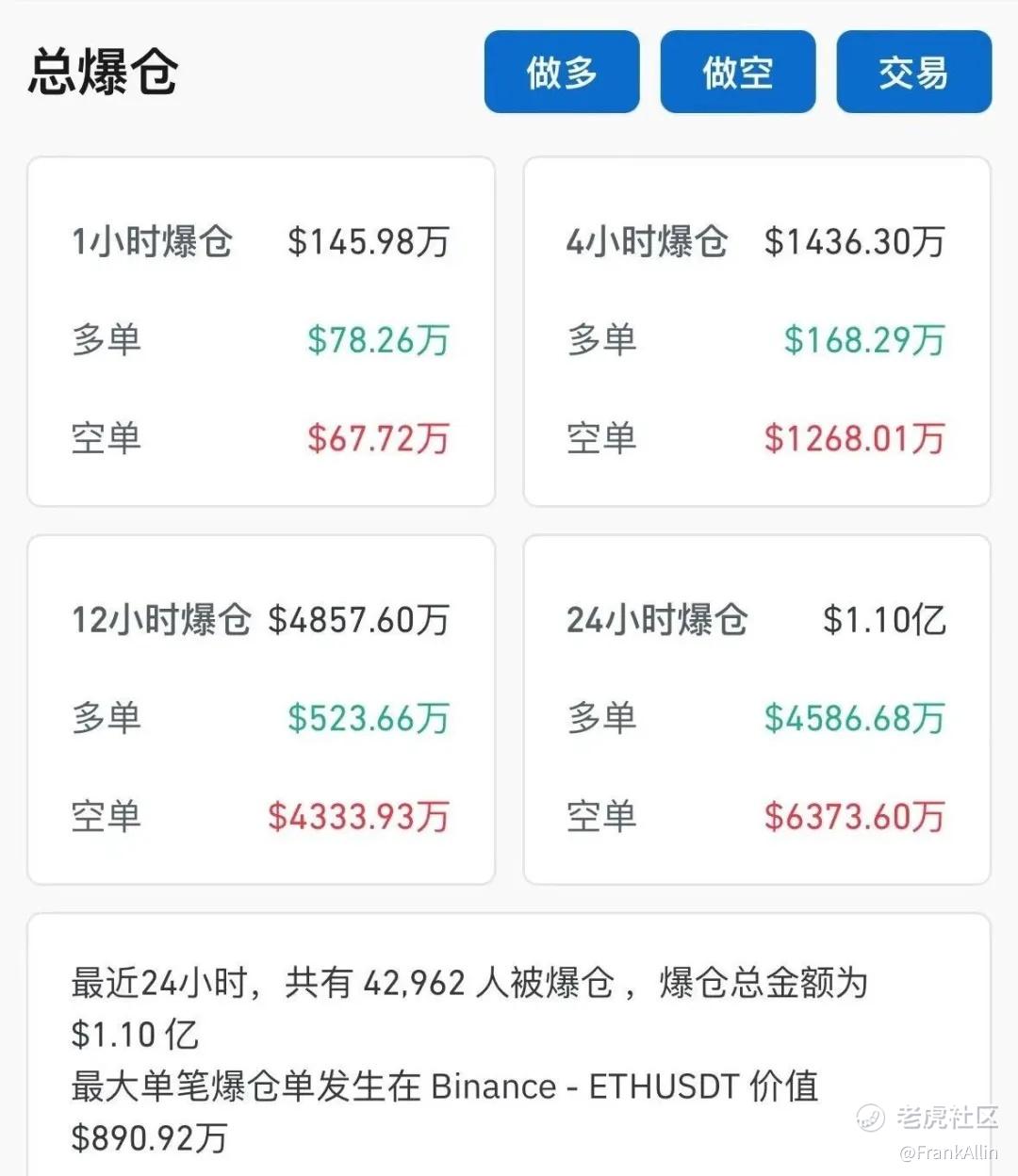
加密货币市场实时爆仓数据统计。在这个市场里，每一刻都有大量参与者爆仓。

而对于市场的单个参与者而言，面对的则是时间概率，一旦在某个节点上爆仓，就彻底出局，再也无法参与市场。

• 平行宇宙

这些年，“平行宇宙”这个概念比较流行。

这一概念其实反映了遍历性的思维。

你是否曾设想过，平行宇宙中的自己，在人生的某个节点上，因选择不同而面对了不一样的结果？

小时候，我们都有过各种梦想，想成为科学家、探险家、作家……

但残酷的是，对于我们个人的人生而言，面对的其实是时间概率。

随着时间的流逝，人生的概率逐渐收敛，每前进一步，就失去了一种可能性。

渐渐地，我们会发现自己的人生是缺乏遍历性的，因为生命时间有限，也因为各种客观条件的限制。

然而，对于社会这个整体而言，是具有遍历性的。

在这个系统中，你会发现你做过的所有梦，仿佛都有人真真切切地在实现着，有人在从事科学探索，有人在探险世界，有人推动社会变革，即使更多的人如我们一样，默默无闻地做着重复劳动的工作。

• 如何在投资中获得遍历性？

时间的切分——重复博弈

在投资中，人们通常会将投资的时间划分为长期和短期。例如，持有股票超过一年通常被称为长期投资，并标榜为价值投资；而持有时间少于一年则被视为短期投机。

但在我这种概率主义者看来，投资时间的长短并无本质区别。

不论是所谓的价值投资，还是短期投机，本质都是概率游戏，只不过面对的概率和赔率结构不同。

一个5年的投资周期中，做一次交易并持有5年的属于长期投资；而同样是5年周期内做500次交易，平均持有周期为2.5天的就不算长期投资了吗？

个人认为，投资没有长期和短期之分，只有操作频率的不同。区别在于是在这个周期里只做一次博弈，还是做500次重复博弈。

重复博弈的意义

在概率游戏的框架中，重复博弈比单次博弈更能使你接近所期望的概率均值。我们都知道，在统计实验中，重复试验能更接近概率均值，而单次实验则更容易出现异常值（outlier）。因此，对于持有周期较长的交易而言，获得概率均值的难度要大得多，被黑天鹅冲击的概率会更高。

从遍历性的角度来看，重复博弈能让你的投资过程尽可能地遍历各种状态，而单次博弈则容易被突发小概率事件所击溃而无法遍历各态。

墨菲定律的存在就说明了这个道理。再小概率的负面事件，在时间拉得足够长的情况下，一定会发生。

时间和概率的关系体现在，随着时间的流逝，概率会趋于收敛，而时间维度的延长，小概率事件发生的可能性会加大。

当我们的操作周期较短时，面对的概率是相对较好估计的；而时间拉长后，在较长的操作周期里，概率变得更难估计，不确定性更高。

回到我们那个投资的公式：

F=P+r×P×t

在这里，时间t是无限可分的，把t分为

t=t1+t2+……tn

那么公式可改为：

F=P×（1+r1）×t1×（1+r2）×t2×……（1+rn）×tn

但在这里，我们面对的还是时间概率。只要在这个链条上的某一个节点上出现-100%的ri收益，爆仓就会发生，你将失去继续参与游戏的权利。

那么，怎么解决这个问题呢？

本金的切分——获得集合概率

让我们再回到赌场的例子。假设一个游戏有10%的爆仓概率，但有90%的概率能获得50%的收益。对于整体的期望值来说，35%的回报率仍然是值得的。

那么，如果我们有100万元，如何参与这个游戏才最合理呢？

我们知道，如果是一个人连续参与这个游戏，最终爆仓的概率是100%。

而如果你雇佣100个人，让这100个人代替你分别拿1万元去参与，尽管有人会爆仓，但这并不会影响其他人获得收益，从而使你能够获得集合概率。

在投资中，我们也可以效仿这种方法。

本金P也是无限可分的。如果我们将本金切分为多个单元，独立参与博弈，就相当于雇佣多个赌徒去参与游戏，而这些单元是相互独立的。某个单元爆仓了，并不会影响其他单元的结果。

用公式表示为：

F=∑ (Pi×（1+ri）×t)

在这里，若有某个ri为-100%，并不会导致整个体系爆仓。

这就是分散投资的意义。通过切分投资本金分散参与游戏，就能获得集合概率，在一定程度上帮助我们增加遍历性。

文章概述了我个人理解的投资体系的底层逻辑。个人的投资体系，就建立在这个逻辑上。

总结一下就是：

• 把投资视为一个概率游戏，选择合适概率和赔率结构的游戏进行下注。

• 让你的投资过程具备遍历性，永远不要爆仓出局。

• 通过重复博弈来获得概率和赔率的均值。

• 分散下注，获得集合概率，增加遍历性。