上一篇提到多因子模型将资产的超额收益率表示为:
式中
为资产n对因子k的暴露度
为因子k的因子收益率
为资产n的特意收益率,即收益率中不能被因子解释的部分
理论有了,作为A股小韭菜怎么将这一模型用于选股呢?本文将尝试用线性回归和逻辑回归算法来解决这一问题。
我们事先准备了79个经单因子分析效果不错的因子,这些因子基本都来自华泰的多因子系列研报。数据获取及预处理过程比较繁琐,与本文主题关系也不太大,大家可以直接下载我处理后的数据。
链接: https://pan.baidu.com/s/1rZYWX-eYvmTyR7pBztGkng?pwd=wpvg 提取码: wpvg
处理方法如下:
1. 股票池:中证500成份股,剔除 ST、PT 股票,剔除上市不满12个月的新股,剔除每个截面期下一交易日停牌的股票。
2. 训练区间:2010-01-01 至 2021-12-31
回测区间:2016-01-01至2022-2-28
3.数据预处理:空值填充、行业市值中性化、中位数去极值、标准化。
4.特征和标签提取:每个自然月的最后一个交易日,计算 79 个因子暴露度,作为样本的原始特征;计算下一整个自然月的个股超额收益(以中证500 指数为基准),作为样本的标签。因子池见下表。
在每个月末截面期,以下个月的个股超额收益率作为标签。
5.训练和测试
样本内训练:每个月使用过去 72 个月的因子数据进行训练,进行月度滚动训练。
样本外测试:模型训练完成后,对接下来的12个月以每月月月末截面期所有样本预处理后的特征作为模型的输入,得到每个样本的预测值,将预测值视作合成后的因子,构建组合进行回测。
先用简单的sklearn.linear_model.LinearRegression测试一下最小二乘法回归(OLS)。它的基本原理是通过在训练数据中拟合线性模型的参数(多因子模型中的
),以最小化数据集中实际的目标与通过线性近似预测的目标之间的残差平方和(MSE)。
基础代码是这样的:
alg = LinearRegression()
alg.fit(X_train, y_train)
alg.predict(X_test)
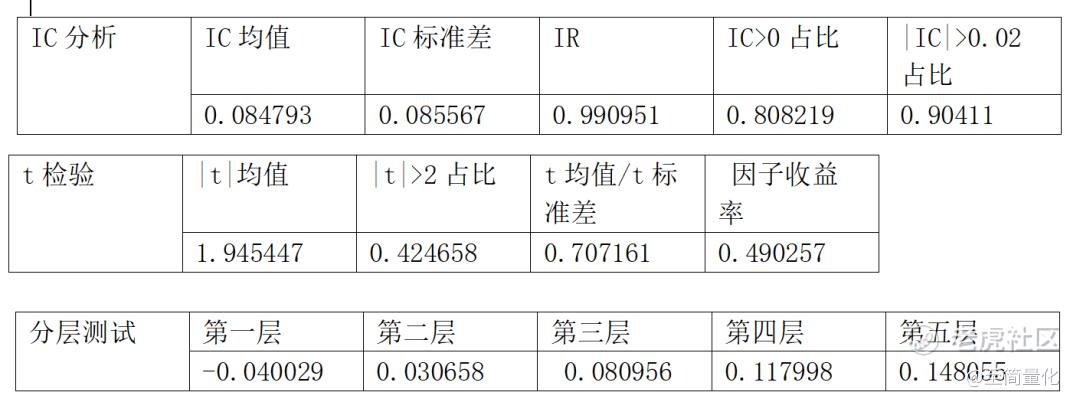
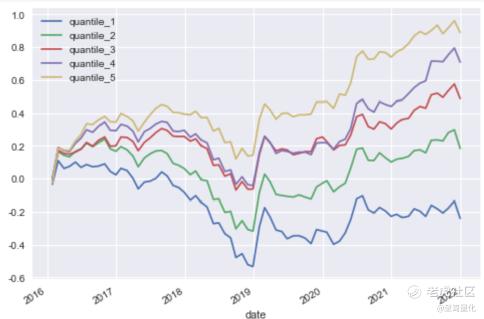
因子分析效果如下:
分层测试走势:
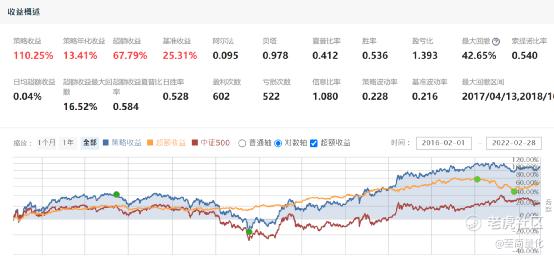
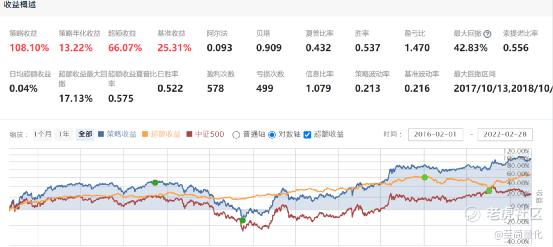
回测效果如下:
万万没想到简单的OLS线性回归结果无论从因子分析还是从回测效果看竟然都还不错。如此简单粗暴的算法都能取得不错的效果,后面要介绍的那一堆机器学习方法会不会更好呢?老实说还真不一定。
下面线性回归模型的正则化版,这类方法也不少,我们选择其中比较简单的一种--岭回归。正则化的线性回归模型就是在线性回归的成本函数里加入正则项,岭回归加入的是是权重向量的l2范数。
基础代码是这样的:
#岭回归模型,设两个参数
alg = Ridge(alpha=10, solver="cholesky")
alg.fit(X_train, y_train)
alg.predict(X_test)
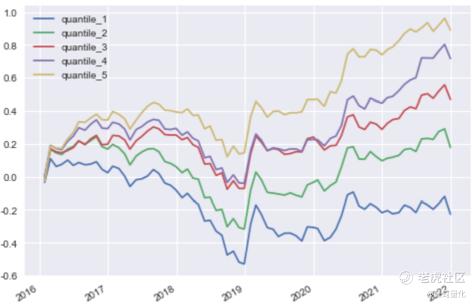
因子分析效果如下:
分层测试走势:
从因子分析结果看与最简单的线性回归模型非常接近,可见优化模型的提升很有限,就不再做进一步的回测了。线性回归就尝试到这里,下面开始尝试用逻辑回归做分类。
数据处理与线性回归都一样,唯一的区别在于数据选取和打标。在每个截面上,选取下月收益排名前 30%的股票设置标签为1, 后 30%的股票设置标签为0。
逻辑回归模型也是计算输入特征的加权和(加上偏置项),但是不同于线性回归模型直接输出结果,它输出的是结果的数理逻辑值。简单说一下逻辑回归的原理,
逻辑回归模型的估计概率
σ是sigmoid函数,
当p~的计算结果小于0.5时,预测结果为0 ,否则为1。
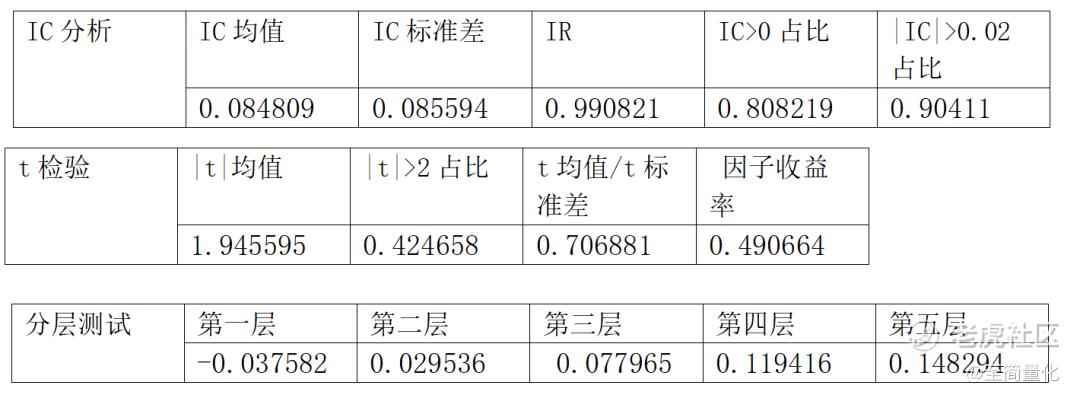
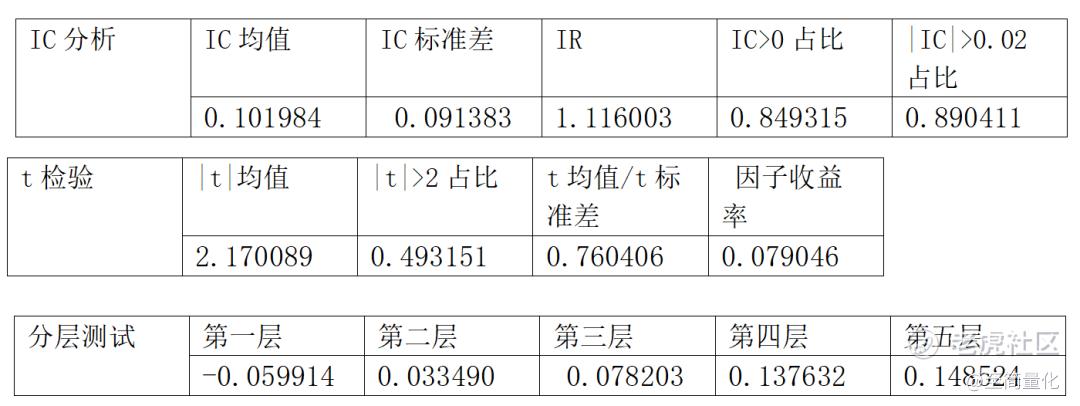
因子分析效果如下:
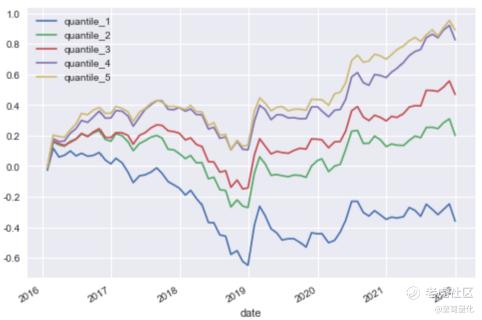
分层测试走势:
回测效果如下:
从IC和t检验的效果看,逻辑回归比线性回归要好不少,但是从分层测试的效果,逻辑回归的优势主要体现在最低层的负收益特别明显,而最高层的正收益相对于线性回归并没有什么提升。这样的优势在只能做多的A股市场不能得到发挥,回测效果也证明了这一点。
这篇文章证明了简单的线性回归和逻辑回归在选股中的效果并不差,不过进一步的提升空间不大。下一篇会尝试更复杂一些的支持向量机和决策树模型。
线性回归代码(逻辑回归类似):
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
import matplotlib.dates as mdates
import matplotlib.pyplot as plt
import seaborn as sns
START_DATE = '2010-01-01'
END_DATE = '2022-01-31'
index ='000905.XSHG'
#print(features)
#features.drop(columns=['INDUSTRY_CODE','market_cap','sqrtcap'],inplace=True)
ind_cap_ret = features[['NEXT_RET','INDUSTRY_CODE','market_cap']]
features.drop(columns=['INDUSTRY_CODE','market_cap'],inplace=True)
#col_list = ['BOOK_TO_PRICE_RATIO', 'GROSS_INCOME_RATIO', 'ROA_TTM', 'EARNINGS_TO_PRICE_RATIO', 'ROE_TTM', 'CASH_EARNINGS_TO_PRICE_RATIO', 'EPCUT', 'gross_profit_margin', 'roe', 'roa', 'adjusted_profit', 'adjusted_profit_ttm', 'opre_yty', 'prof_yty', 'roe_yty', 'alpha', 'return_1m', 'return_3m', 'return_6m', 'wgt_return_1m', 'wgt_return_3m', 'wgt_return_6m', 'wgt_return_12m', 'exp_wgt_return_1m', 'exp_wgt_return_3m', 'exp_wgt_return_6m', 'exp_wgt_return_12m', 'dp', 'ff_rsd_std_1m', 'ff_rsd_std_3m', 'ff_rsd_std_6m', 'std_1m', 'std_3m', 'std_6m', 'std_12m', 'ln_price', 'turn_1m', 'turn_3m', 'turn_6m', 'turn_12m', 'bias_turn_1m', 'bias_turn_3m', 'bias_turn_6m', 'bias_turn_12m', 'PSY', 'RSI', 'BIAS', 'DIF', 'DEA', 'MACD', 'per_holder_chg', 'alpha_003', 'alpha_013', 'alpha_016', 'alpha_055', 'alpha_044', 'alpha_050', 'alpha_015', 'rank_EP_2', 'rank_roa_6', 'rank_gross_profit_margin_6']
#features = features[col_list]
features_sample = features.rename(columns={"NEXT_RET": "label"})
#测试用,没有做特征选择-线性回归
dates = features_sample.index.levels[0]
predic=pd.DataFrame()
start_year = int(dates[0].strftime('%Y'))
for i in range(0,1000):
# 72个月的训练数据
start_date =pd.Timestamp(year=start_year+i, month=1, day=1)
end_date =pd.Timestamp(year=start_year +i+5, month=12, day=1)
print('train dates')
print(dates[(dates>=start_date) & (dates<=end_date)])
sample_data_72_extra=features_sample.loc[dates[(dates>=start_date) & (dates<=end_date)]]
y_train = sample_data_72_extra['label'] # 分割y
X_train = sample_data_72_extra.drop(columns=['label'])
#线性回归模型,全部采用默认参数
alg = LinearRegression()
alg.fit(X_train, y_train)
# 预测集数据
start_date =pd.Timestamp(year=start_year +i+6, month=1, day=1)
end_date =pd.Timestamp(year=start_year +i+6, month=12, day=31)
# 取训练数据先一年的数据作为样本外数据特征
for date in dates[(dates>=start_date) & (dates<=end_date)]:
test_data=features.loc[date]
X_test = test_data.copy()
del X_test['NEXT_RET']
#Predict predict set:
predc_pred = pd.DataFrame(alg.predict(X_test), columns=['linear-proba']) # 获得预测
predc_pred['date'] = date
predc_pred['code'] = X_test.index
predc_pred.set_index(['date','code'],inplace=True)
predic = pd.concat([predic,predc_pred], axis=0)
if end_date>=dates[-1]:
break
predic = predic.merge(ind_cap_ret, how='inner', left_index=True, right_index=True)
predic.to_csv(the_path+'predic-linear-proba.csv')

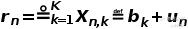
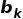
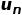
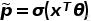
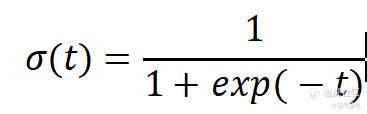

精彩评论